Products: Abaqus/Standard Abaqus/Explicit Abaqus/CAE
Material damping can be defined:
for direct-integration (nonlinear, implicit or explicit), subspace-based direct-integration, direct-solution steady-state, and subspace-based steady-state dynamic analysis; or
for mode-based (linear) dynamic analysis in Abaqus/Standard.
In direct-integration dynamic analysis you very often define energy dissipation mechanisms—dashpots, inelastic material behavior, etc.—as part of the basic model. In such cases there is usually no need to introduce additional damping: it is often unimportant compared to these other dissipative effects. However, some models do not have such dissipation sources (an example is a linear system with chattering contact, such as a pipeline in a seismic event). In such cases it is often desirable to introduce some general damping. Abaqus provides “Rayleigh” damping for this purpose. It provides a convenient abstraction to damp lower (mass-dependent) and higher (stiffness-dependent) frequency range behavior.
Rayleigh damping can also be used in direct-solution steady-state dynamic analyses and subspace-based steady-state dynamic analyses to get quantitatively accurate results, especially near natural frequencies.
To define Rayleigh damping, you specify two Rayleigh damping factors: 
for mass proportional damping and 
for stiffness proportional damping. In general, damping is a material property specified as part of the material definition. For the cases of rotary inertia, point mass elements, and substructures, where there is no reference to a material definition, the damping can be defined in conjunction with the property references. Any mass proportional damping also applies to nonstructural features (see “Nonstructural mass definition,” Section 2.7.1).
For a given mode i the fraction of critical damping, 
, can be expressed in terms of the damping factors and as:
is the natural frequency at this mode. This equation implies that, generally speaking, the mass proportional Rayleigh damping, , damps the lower frequencies and the stiffness proportional Rayleigh damping, , damps the higher frequencies.The factor introduces damping forces caused by the absolute velocities of the model and so simulates the idea of the model moving through a viscous “ether” (a permeating, still fluid, so that any motion of any point in the model causes damping). This damping factor defines mass proportional damping, in the sense that it gives a damping contribution proportional to the mass matrix for an element. If the element contains more than one material in Abaqus/Standard, the volume average value of is used to multiply the element's mass matrix to define the damping contribution from this term. If the element contains more than one material in Abaqus/Explicit, the mass average value of is used to multiply the element's lumped mass matrix to define the damping contribution from this term. has units of (1/time).
| Input File Usage: | *DAMPING, ALPHA= |
| Abaqus/CAE Usage: | Property module: material editor: Mechanical |
The factor introduces damping proportional to the strain rate, which can be thought of as damping associated with the material itself. defines damping proportional to the elastic material stiffness. Since the model may have quite general nonlinear response, the concept of “stiffness proportional damping” must be generalized, since it is possible for the tangent stiffness matrix to have negative eigenvalues (which would imply negative damping). To overcome this problem, is interpreted as defining viscous material damping in Abaqus, which creates an additional “damping stress,” 
, proportional to the total strain rate:
is the strain rate. For hyperelastic (“Hyperelastic behavior of rubberlike materials,” Section 21.5.1) and hyperfoam (“Hyperelastic behavior in elastomeric foams,” Section 21.5.2) materials 
is defined as the elastic stiffness in the strain-free state. For all other linear elastic materials in Abaqus/Standard and all other materials in Abaqus/Explicit, is the material's current elastic stiffness. will be calculated based on the current temperature during the analysis.This damping stress is added to the stress caused by the constitutive response at the integration point when the dynamic equilibrium equations are formed, but it is not included in the stress output. As a result, damping can be introduced for any nonlinear case and provides standard Rayleigh damping for linear cases; for a linear case stiffness proportional damping is exactly the same as defining a damping matrix equal to times the (elastic) material stiffness matrix. Other contributions to the stiffness matrix (e.g., hourglass, transverse shear, and drill stiffnesses) are not included when computing stiffness proportional damping. has units of (time).
| Input File Usage: | *DAMPING, BETA= |
| Abaqus/CAE Usage: | Property module: material editor: Mechanical |
Structural damping assumes that the damping forces are proportional to the forces caused by stressing of the structure and are opposed to the velocity. Therefore, this form of damping can be used only when the displacement and velocity are exactly 90° out of phase. Structural damping is best suited for frequency domain dynamic procedures (see “Damping in modal superposition procedures” below). The damping forces are then
are the damping forces, 
, s is the user-defined structural damping factor, and 
are the forces caused by stressing of the structure. The damping forces due to structural damping are intended to represent frictional effects (as distinct from viscous effects). Thus, structural damping is suggested for models involving materials that exhibit frictional behavior or where local frictional effects are present throughout the model, such as dry rubbing of joints in a multi-link structure.Structural damping can be added to the model as mechanical dampers such as connector damping or as a complex stiffness on spring elements.
Structural damping can be used in steady-state dynamic procedures that allow for nondiagonal damping.
| Input File Usage: | Use the following option to define structural damping: |
*DAMPING, STRUCTURAL= |
| Abaqus/CAE Usage: | Property module: material editor: Mechanical |
In Abaqus/Standard the operators used for implicit direct time integration introduce some artificial damping in addition to Rayleigh damping. Damping associated with the Hilber-Hughes-Taylor and hybrid operators is usually controlled by the Hilber-Hughes-Taylor parameter 
, which is not the same as the parameter controlling the mass proportional part of Rayleigh damping. The 
and 
parameters of the Hilber-Hughes-Taylor and hybrid operators also affect numerical damping. The , , and parameters are not available for the backward Euler operator. See “Implicit dynamic analysis using direct integration,” Section 6.3.2, for more information about this other form of damping.
Rayleigh damping is meant to reflect physical damping in the actual material. In Abaqus/Explicit a small amount of numerical damping is introduced by default in the form of bulk viscosity to control high frequency oscillations; see “Explicit dynamic analysis,” Section 6.3.3, for more information about this other form of damping.
As the fraction of critical damping for the highest mode (
) increases, the stable time increment for Abaqus/Explicit decreases according to the equation
, the frequency of the highest mode, into the equation for given previously)
To illustrate the effect that damping has on the stable time increment, consider a cantilever in bending modeled with continuum elements. The lowest frequency is 
1 rad/sec, while for the particular mesh chosen, the highest frequency is 
1000 rad/sec. The lowest mode in this problem corresponds to the cantilever in bending, and the highest frequency is related to the dilation of a single element.
With no damping the stable time increment is
However, if we use mass proportional damping to damp out the lowest mode with 1% of critical damping, the damping factor is given by
This example demonstrates that it is generally preferable to damp out low frequency response with mass proportional damping rather than stiffness proportional damping. However, mass proportional damping can significantly affect rigid body motion, so large is often undesirable. To avoid a dramatic drop in the stable time increment, the stiffness proportional damping factor, , should be less than or of the same order of magnitude as the initial stable time increment without damping. With 
, the stable time increment is reduced by about 52%.
Damping can be specified as part of the step definition for the following modal superposition procedures:
Fraction of critical damping
Rayleigh damping
Composite modal damping
Structural damping
You can specify the damping in each eigenmode in the model or for the specified frequency as a fraction of the critical damping. Critical damping is defined as
, are from 1% to 10% of critical damping, 
; but Abaqus/Standard accepts any positive value. The critical damping factors can be changed from step to step.| Input File Usage: | Use the following option to define damping by specifying mode numbers: |
*MODAL DAMPING, MODAL=DIRECT, DEFINITION=MODE NUMBERS Use the following option to define damping by specifying a frequency range: *MODAL DAMPING, MODAL=DIRECT, DEFINITION=FREQUENCY RANGE |
| Abaqus/CAE Usage: | Use the following input to define damping by specifying mode numbers: |
Step module: Create Step: Linear perturbation: any valid step type: Damping: Specify damping over ranges of: Modes, Direct modal: Use direct damping data Use the following input to define damping by specifying frequency ranges: Step module: Create Step: Linear perturbation: any valid step type: Damping: Specify damping over ranges of: Frequencies, Direct modal: Use direct damping data |
For uncoupled structural-acoustic frequency extractions performed using the AMS eigensolver, you can apply different damping to the structural and acoustic modes. This technique can be used only when damping is specified for a range of frequencies.
| Input File Usage: | Use the following option to apply the specified damping to only the structural modes: |
*MODAL DAMPING, MODAL=DIRECT, DEFINITION=FREQUENCY RANGE, FIELD=MECHANICAL Use the following option to apply the specified damping to only the acoustic modes: *MODAL DAMPING, MODAL=DIRECT, DEFINITION=FREQUENCY RANGE, FIELD=ACOUSTIC Use the following option to apply the specified damping to both structural and acoustic modes (default): *MODAL DAMPING, MODAL=DIRECT, DEFINITION=FREQUENCY RANGE, FIELD=ALL |
| Abaqus/CAE Usage: | The ability to specify different damping for structural and acoustic modes is not supported in Abaqus/CAE. |
Rayleigh damping introduces a damping matrix, 
, defined as
is the mass matrix of the model, 
is the stiffness matrix of the model, and and are factors that you define.In Abaqus/Standard you can define and independently for each mode, so that the above equation becomes
, 
, and 
are the damping, mass, and stiffness terms associated with the Mth mode.| Input File Usage: | Use the following option to define damping by specifying mode numbers: |
*MODAL DAMPING, RAYLEIGH, DEFINITION=MODE NUMBERS Use the following option to define damping by specifying a frequency range: *MODAL DAMPING, RAYLEIGH, DEFINITION=FREQUENCY RANGE |
| Abaqus/CAE Usage: | Use the following input to define damping by specifying mode numbers: |
Step module: Create Step: Linear perturbation: any valid step type: Damping: Specify damping over ranges of: Modes, Rayleigh: Use Rayleigh damping data Use the following input to define damping by specifying frequency ranges: Step module: Create Step: Linear perturbation: any valid step type: Damping: Specify damping over ranges of: Frequencies, Rayleigh: Use Rayleigh damping data |
Composite modal damping allows you to define a damping factor for each material in the model as a fraction of critical damping. These factors are then combined into a damping factor for each mode as weighted averages of the mass matrix associated with each material:
is the critical damping fraction used in mode , 
is the critical damping fraction defined for material m, 
is the mass matrix associated with material m, 
is the eigenvector of mode , and 
is the generalized mass associated with mode : 
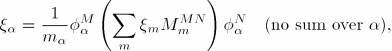
If you specify composite modal damping, Abaqus calculates the damping coefficients in the eigenfrequency extraction step from the damping factors that you defined for each material. Composite modal damping can be defined only by specifying mode numbers; it cannot be defined by specifying a frequency range.
| Input File Usage: | Use both of the following options: |
*DAMPING, COMPOSITE= |
| Abaqus/CAE Usage: | Property module: material editor: Mechanical |
Structural damping assumes that the damping forces are proportional to the forces caused by stressing of the structure and are opposed to the velocity (see “Structural damping” above for more information). This form of damping can be used only when the displacement and velocity are exactly 90° out of phase, as in steady-state and random response analyses where the excitation is purely sinusoidal.
Structural damping can be defined as diagonal modal damping for mode-based steady-state dynamic and random response analyses. For more information about defining structural damping at the global level or at the material level for steady-state dynamic procedures that allow nondiagonal damping, see “Damping in dynamic analysis” in “Dynamic analysis procedures: overview,” Section 6.3.1.
| Input File Usage: | Use the following option to define damping by specifying mode numbers: |
*MODAL DAMPING, STRUCTURAL, DEFINITION=MODE NUMBERS Use the following option to define damping by specifying a frequency range: *MODAL DAMPING, STRUCTURAL, DEFINITION=FREQUENCY RANGE |
| Abaqus/CAE Usage: | Use the following input to define damping by specifying mode numbers: |
Step module: Create Step: Linear perturbation: any valid step type: Damping: Specify damping over ranges of: Modes, Structural: Use structural damping data Use the following input to define damping by specifying frequency ranges: Step module: Create Step: Linear perturbation: any valid step type: Damping: Specify damping over ranges of: Frequencies, Structural: Use structural damping data |
The factor applies to all elements that use a linear elastic material definition (“Linear elastic behavior,” Section 21.2.1) and to Abaqus/Standard beam and shell elements that use general sections. In the latter case, if a nonlinear beam section definition is provided, the factor is multiplied by the slope of the force-strain (or moment-curvature) relationship at zero strain or curvature. In addition, the factor applies to all Abaqus/Explicit elements that use a hyperelastic material definition (“Hyperelastic behavior of rubberlike materials,” Section 21.5.1), a hyperfoam material definition (“Hyperelastic behavior in elastomeric foams,” Section 21.5.2), or general shell sections (“Using a general shell section to define the section behavior,” Section 28.6.6).
In the case of a no tension elastic material the factor is not used in tension, while for a no compression elastic material the factor is not used in compression (see “No compression or no tension,” Section 21.2.2). In other words, these modified elasticity models exhibit damping only when they have stiffness.
The factor is applied to all elements that have mass including point mass elements in Abaqus/Standard and excluding point mass elements in Abaqus/Explicit (where, if required, discrete DASHPOTA elements in each global direction, each with one node fixed, can be used to introduce this type of damping). For point mass and rotary inertia elements in Abaqus/Standard mass proportional or composite modal damping are defined as part of the point mass or rotary inertia definitions (“Point masses,” Section 29.1.1, and “Rotary inertia,” Section 29.2.1). This factor is not available for rotary inertia elements in Abaqus/Explicit.
The factor is not available for spring elements: discrete dashpot elements should be used in parallel with spring elements instead.
The factor is also not applied to the transverse shear terms in Abaqus/Standard beams and shells.
In Abaqus/Standard composite modal damping cannot be used with or within substructures. Rayleigh damping can be introduced for substructures. When Rayleigh damping is used within a substructure, and are averaged over the substructure to define single values of and for the substructure. These are weighted averages, using the mass as the weighting factor for and the volume as the weighting factor for . These averaged damping values can be superseded by providing them directly in a second damping definition. See “Using substructures,” Section 10.1.1.
