Products: Abaqus/Standard Abaqus/CAE Abaqus/Viewer
Modeling discontinuities, such as cracks, as an enriched feature:
is commonly referred to as the extended finite element method (XFEM);
is an extension of the conventional finite element method based on the concept of partition of unity;
allows the presence of discontinuities in an element by enriching degrees of freedom with special displacement functions;
does not require the mesh to match the geometry of the discontinuities;
is a very attractive and effective way to simulate initiation and propagation of a discrete crack along an arbitrary, solution-dependent path without the requirement of remeshing in the bulk materials;
can be simultaneously used with the surface-based cohesive behavior approach (see “Surface-based cohesive behavior,” Section 35.1.10) or the Virtual Crack Closure Technique (see “Crack propagation analysis,” Section 11.4.3), which are best suited for modeling interfacial delamination;
can be performed using the static procedure (see “Static stress analysis,” Section 6.2.2), the implicit dynamic procedure (see “Implicit dynamic analysis using direct integration,” Section 6.3.2), or the low-cycle fatigue analysis using the direct cyclic approach (see “Low-cycle fatigue analysis using the direct cyclic approach,” Section 6.2.7);
can also be used to perform contour integral evaluations for an arbitrary stationary surface crack without the need to refine the mesh around the crack tip;
allows contact interaction of cracked element surfaces based on a small-sliding formulation;
allows both material and geometrical nonlinearity; and
is currently available only for first-order stress/displacement solid continuum elements and second-order stress/displacement tetrahedron elements.
Modeling stationary discontinuities, such as a crack, with the conventional finite element method requires that the mesh conforms to the geometric discontinuities. Therefore, considerable mesh refinement is needed in the neighborhood of the crack tip to capture the singular asymptotic fields adequately. Modeling a growing crack is even more cumbersome because the mesh must be updated continuously to match the geometry of the discontinuity as the crack progresses.
The extended finite element method (XFEM) alleviates the shortcomings associated with meshing crack surfaces. The extended finite element method was first introduced by Belytschko and Black (1999). It is an extension of the conventional finite element method based on the concept of partition of unity by Melenk and Babuska (1996), which allows local enrichment functions to be easily incorporated into a finite element approximation. The presence of discontinuities is ensured by the special enriched functions in conjunction with additional degrees of freedom. However, the finite element framework and its properties such as sparsity and symmetry are retained.
For the purpose of fracture analysis, the enrichment functions typically consist of the near-tip asymptotic functions that capture the singularity around the crack tip and a discontinuous function that represents the jump in displacement across the crack surfaces. The approximation for a displacement vector function 
with the partition of unity enrichment is
are the usual nodal shape functions; the first term on the right-hand side of the above equation, 
, is the usual nodal displacement vector associated with the continuous part of the finite element solution; the second term is the product of the nodal enriched degree of freedom vector, 
, and the associated discontinuous jump function 
across the crack surfaces; and the third term is the product of the nodal enriched degree of freedom vector, 
, and the associated elastic asymptotic crack-tip functions, 
. The first term on the right-hand side is applicable to all the nodes in the model; the second term is valid for nodes whose shape function support is cut by the crack interior; and the third term is used only for nodes whose shape function support is cut by the crack tip. Figure 10.7.1–1 illustrates the discontinuous jump function across the crack surfaces, , which is given by 
is a sample (Gauss) point, 
is the point on the crack closest to , and 
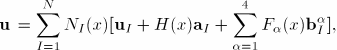
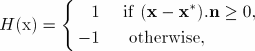
is the unit outward normal to the crack at . Figure 10.7.1–1 illustrates the asymptotic crack tip functions in an isotropic elastic material, , which are given by
is a polar coordinate system with its origin at the crack tip and 
is tangent to the crack at the tip. These functions span the asymptotic crack-tip function of elasto-statics, and 
takes into account the discontinuity across the crack face. The use of asymptotic crack-tip functions is not restricted to crack modeling in an isotropic elastic material. The same approach can be used to represent a crack along a bimaterial interface, impinged on the bimaterial interface, or in an elastic-plastic power law hardening material. However, in each of these three cases different forms of asymptotic crack-tip functions are required depending on the crack location and the extent of the inelastic material deformation. The different forms for the asymptotic crack-tip functions are discussed by Sukumar (2004), Sukumar and Prevost (2003), and Elguedj (2006), respectively.
Accurately modeling the crack-tip singularity requires constantly keeping track of where the crack propagates and is cumbersome because the degree of crack singularity depends on the location of the crack in a non-isotropic material. Therefore, we consider the asymptotic singularity functions only when modeling stationary cracks in Abaqus/Standard. Moving cracks are modeled using one of the two alternative approaches described below.
One alternative approach within the framework of XFEM is based on traction-separation cohesive behavior. This approach is used in Abaqus/Standard to simulate crack initiation and propagation. This is a very general interaction modeling capability, which can be used for modeling brittle or ductile fracture. The other crack initiation and propagation capabilities available in Abaqus/Standard are based on cohesive elements (“Defining the constitutive response of cohesive elements using a traction-separation description,” Section 31.5.6) or on surface-based cohesive behavior (“Surface-based cohesive behavior,” Section 35.1.10). Unlike these methods, which require that the cohesive surfaces align with element boundaries and the cracks propagate along a set of predefined paths, the XFEM-based cohesive segments method can be used to simulate crack initiation and propagation along an arbitrary, solution-dependent path in the bulk materials, since the crack propagation is not tied to the element boundaries in a mesh. In this case the near-tip asymptotic singularity is not needed, and only the displacement jump across a cracked element is considered. Therefore, the crack has to propagate across an entire element at a time to avoid the need to model the stress singularity.
Phantom nodes, which are superposed on the original real nodes, are introduced to represent the discontinuity of the cracked elements, as illustrated in Figure 10.7.1–2. When the element is intact, each phantom node is completely constrained to its corresponding real node. When the element is cut through by a crack, the cracked element splits into two parts. Each part is formed by a combination of some real and phantom nodes depending on the orientation of the crack. Each phantom node and its corresponding real node are no longer tied together and can move apart.
The magnitude of the separation is governed by the cohesive law until the cohesive strength of the cracked element is zero, after which the phantom and the real nodes move independently. To have a set of full interpolation bases, the part of the cracked element that belongs in the real domain, 
, is extended to the phantom domain, 
. Then the displacement in the real domain, , can be interpolated by using the degrees of freedom for the nodes in the phantom domain, . The jump in the displacement field is realized by simply integrating only over the area from the side of the real nodes up to the crack; i.e., 
and 
. This method provides an effective and attractive engineering approach and has been used for simulation of the initiation and growth of multiple cracks in solids by Song (2006) and Remmers (2008). It has been proven to exhibit almost no mesh dependence if the mesh is sufficiently refined.
Another alternative approach to modeling moving cracks within the framework of XFEM is based on the principles of linear elastic fracture mechanics (LEFM). Therefore, it is more appropriate for problems in which brittle crack propagation occurs. Similar to the XFEM-based cohesive segments method described above, the near-tip asymptotic singularity is not considered, and only the displacement jump across a cracked element is considered. Therefore, the crack has to propagate across an entire element at a time to avoid the need to model the stress singularity. The strain energy release rate at the crack tip is calculated based on the modified Virtual Crack Closure Technique (VCCT), which has been used to model delamination along a known and partially bonded surface (see “Crack propagation analysis,” Section 11.4.3). However, unlike this method, the XFEM-based LEFM approach can be used to simulate crack propagation along an arbitrary, solution-dependent path in the bulk material without the requirement of a pre-existing crack in the model.
The modeling technique is very similar to the XFEM-based cohesive segment approach described above where phantom nodes are introduced to represent the discontinuity of the cracked element when the fracture criterion is satisfied. The real node and the corresponding phantom node will separate when the equivalent strain energy release rate exceeds the critical strain energy release rate at the crack tip in an enriched element. The traction is initially carried as equal and opposite forces on the two surfaces of the cracked element. The traction is ramped down linearly over the separation between the two surfaces with the dissipated strain energy equal to the critical strain energy required to initiate the separation.
The XFEM-based LEFM approach can also be used to simulate a discrete crack growth subjected to sub-critical cyclic loading in a low-cycle fatigue analysis using the direct cyclic approach (“Low-cycle fatigue analysis using the direct cyclic approach,” Section 6.2.7). The fracture energy release rates at the crack tips in the enriched elements are calculated based on the above mentioned modified VCCT technique. The onset and crack growth are characterized by using the Paris law, which relates the relative fracture energy release rates to crack growth rates as illustrated in Figure 10.7.1–3. This approach has been used to model progressive delamination under a sub-critical cyclic loading along a known and partially bonded surface (see “Low-cycle fatigue criterion” in “Crack propagation analysis,” Section 11.4.3). However, unlike this method, the XFEM-based LEFM approach can be used to simulate fatigue crack propagation along an arbitrary, solution-dependent path in the bulk material.
A key development that facilitates treatment of cracks in an extended finite element analysis is the description of crack geometry, because the mesh is not required to conform to the crack geometry. The level set method, which is a powerful numerical technique for analyzing and computing interface motion, fits naturally with the extended finite element method and makes it possible to model arbitrary crack growth without remeshing. The crack geometry is defined by two almost-orthogonal signed distance functions, as illustrated in Figure 10.7.1–4. The first, 
, describes the crack surface, while the second, 
, is used to construct an orthogonal surface so that the intersection of the two surfaces gives the crack front. 
indicates the positive normal to the crack surface; 
indicates the positive normal to the crack front. No explicit representation of the boundaries or interfaces is needed because they are entirely described by the nodal data. Two signed distance functions per node are generally required to describe a crack geometry.
You must specify an enriched feature and its properties. One or multiple pre-existing cracks can be associated with an enriched feature. In addition, during an analysis one or multiple cracks can initiate in an enriched feature without any initial defects. However, multiple cracks can nucleate in a single enriched feature only when the damage initiation criterion is satisfied in multiple elements in the same time increment. Otherwise, additional cracks will not nucleate until all the pre-existing cracks in an enriched feature have propagated through the boundary of the given enriched feature. If several crack nucleations are expected to occur at different locations sequentially during an analysis, multiple enriched features can be specified in the model. Enriched degrees of freedom are activated only when an element is intersected by a crack. Only stress/displacement solid continuum elements can be associated with an enriched feature.
| Input File Usage: | *ENRICHMENT |
| Abaqus/CAE Usage: | Interaction module: Special |
You can choose to model an arbitrary stationary crack or a discrete crack propagation along an arbitrary, solution-dependent path. The former requires that the elements around the crack tips are enriched with asymptotic functions to catch the singularity and that the elements intersected by the crack interior are enriched with the jump function across the crack surfaces. The latter infers that crack propagation is modeled with either the cohesive segments method or the linear elastic fracture mechanics approach in conjunction with phantom nodes. However, the options are mutually exclusive and cannot be specified simultaneously in a model.
| Input File Usage: | Use the following option to specify a crack propagation analysis (default): |
*ENRICHMENT, TYPE=PROPAGATION CRACK Use the following option to specify an analysis with stationary cracks: *ENRICHMENT, TYPE=STATIONARY CRACK |
| Abaqus/CAE Usage: | Use the following input to specify a crack propagation analysis: |
Interaction module: crack editor: toggle on Allow crack growth Use the following input to specify an analysis with stationary cracks: Interaction module: crack editor: toggle off Allow crack growth |
You must assign a name to an enriched feature, such as a crack. This name can be used in defining the initial location of the crack surfaces, in identifying a crack for contour integral output, and in activating or deactivating the crack propagation analysis.
| Input File Usage: | *ENRICHMENT, NAME=name |
| Abaqus/CAE Usage: | Interaction module: Special |
You must associate the enrichment definition with a region of your model. Only degrees of freedom in elements within these regions are potentially enriched with special functions. The region should consist of elements that are presently intersected by cracks and those that are likely to be intersected by cracks as the cracks propagate.
| Input File Usage: | *ENRICHMENT, ELSET=element set name |
| Abaqus/CAE Usage: | Interaction module: Special |
When an element is cut by a crack, the compressive behavior of the crack surfaces has to be considered. The formulae that govern behavior are very similar to those used for surface-based small-sliding penalty contact (“Mechanical contact properties: overview,” Section 35.1.1). However, the frictional behavior is not yet considered in the shear direction.
For an element intersected by a stationary crack or a moving crack with the linear elastic fracture mechanics approach, it is assumed that the elastic cohesive strength of the cracked element is zero. Therefore, compressive behavior of the crack surfaces is fully defined with the above options when the crack surfaces come into contact. For a moving crack with the cohesive segments method, the situation is more complex; traction-separation cohesive behavior as well as compressive behavior of the crack surfaces are involved in a cracked element. In the contact normal direction, the pressure-overclosure relationship governing the compressive behavior between the surfaces does not interact with the cohesive behavior, since they each describe the interaction between the surfaces in a different contact regime. The pressure-overclosure relationship governs the behavior only when the crack is “closed”; the cohesive behavior contributes to the contact normal stress only when the crack is “open” (i.e., not in contact).
If the elastic cohesive stiffness of an element is undamaged in the shear direction, it is assumed that the cohesive behavior is active. Any tangential slip is assumed to be purely elastic in nature and is resisted by the elastic cohesive strength of the element, resulting in shear forces. If damage has been defined, the cohesive contribution to the shear stresses starts degrading with damage evolution. Once maximum degradation has been reached, the cohesive contribution to the shear stresses is zero.
| Input File Usage: | Use the following options to define contact of crack surfaces using a small-sliding formulation: |
*ENRICHMENT, INTERACTION=interaction_property_name *SURFACE INTERACTION, NAME=interaction_property_name *SURFACE BEHAVIOR |
| Abaqus/CAE Usage: | Interaction module: crack editor: toggle on Specify contact property |
The formulae and laws that govern the behavior of XFEM-based cohesive segments for a crack propagation analysis are very similar to those used for cohesive elements with traction-separation constitutive behavior (“Defining the constitutive response of cohesive elements using a traction-separation description,” Section 31.5.6) and those used for surface-based cohesive behavior (“Surface-based cohesive behavior,” Section 35.1.10). The similarities extend to the linear elastic traction-separation model, damage initiation criteria, and damage evolution laws.
The available traction-separation model in Abaqus assumes initially linear elastic behavior followed by the initiation and evolution of damage. The elastic behavior is written in terms of an elastic constitutive matrix that relates the normal and shear stresses to the normal and shear separations of a cracked element.
The nominal traction stress vector, 
, consists of the following components: 
, 
, and (in three-dimensional problems) 
, which represent the normal and the two shear tractions, respectively. The corresponding separations are denoted by 
, 
, and 
. The elastic behavior can then be written as
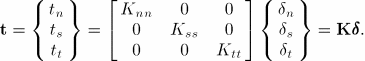
The normal and tangential stiffness components will not be coupled: pure normal separation by itself does not give rise to cohesive forces in the shear directions, and pure shear slip with zero normal separation does not give rise to any cohesive forces in the normal direction.
The terms 
, 
, and 
are calculated based on the elastic properties for an enriched element. Specifying the elastic properties of the material in an enriched region is sufficient to define both the elastic stiffness and the traction-separation behavior.
Damage modeling allows you to simulate the degradation and eventual failure of an enriched element. The failure mechanism consists of two ingredients: a damage initiation criterion and a damage evolution law. The initial response is assumed to be linear as discussed in the previous section. However, once a damage initiation criterion is met, damage can occur according to a user-defined damage evolution law. Figure 10.7.1–5 shows a typical linear and a typical nonlinear traction-separation response with a failure mechanism. The enriched elements do not undergo damage under pure compression.
Damage of the traction-separation response for cohesive behavior in an enriched element is defined within the same general framework used for conventional materials (see “Progressive damage and failure,” Section 23.1.1). However, unlike cohesive elements with traction-separation behavior, you do not have to specify the undamaged traction-separation behavior in an enriched element.
Crack initiation refers to the beginning of degradation of the cohesive response at an enriched element. The process of degradation begins when the stresses or the strains satisfy specified crack initiation criteria. Crack initiation criteria are available based on the following Abaqus/Standard built-in models:
the maximum principal stress criterion,
the maximum principal strain criterion,
the maximum nominal stress criterion,
the maximum nominal strain criterion,
the quadratic traction-interaction criterion, and
the quadratic separation-interaction criterion.
An additional crack is introduced or the crack length of an existing crack is extended after an equilibrium increment when the fracture criterion, f, reaches the value 1.0 within a given tolerance:
. If 
, the time increment is cut back such that the crack initiation criterion is satisfied. The default value of is 0.05.| Input File Usage: | *DAMAGE INITIATION, TOLERANCE= |
| Abaqus/CAE Usage: | Property module: material editor: Mechanical: Damage for Traction Separation Laws: Quade Damage, Maxe Damage, Quads Damage, Maxs Damage, Maxpe Damage, or Maxps Damage: Tolerance: |
When the maximum principal stress or the maximum principal strain criterion is specified, the newly introduced crack is always orthogonal to the maximum principal stress/strain direction when the fracture criterion is satisfied. However, when one of the other Abaqus/Standard built-in crack initiation criteria is used, you have to specify if the newly introduced crack will be orthogonal to the element local 1-direction or orthogonal to the element local 2-direction (see “Conventions,” Section 1.2.2) when the fracture criterion is satisfied. By default, the crack is orthogonal to the element local 1-direction. If a user-defined damage initiation criterion is specified, the normal direction to the crack plane or the crack line can be defined in user subroutine UDMGINI.
| Input File Usage: | Use one of the following options to specify the crack direction when the maximum nominal stress, the maximum nominal strain, the quadratic traction-interaction, or the quadratic separation-interaction criterion is specified: |
*DAMAGE INITIATION, NORMAL DIRECTION=1 (default) *DAMAGE INITIATION, NORMAL DIRECTION=2 |
| Abaqus/CAE Usage: | Property module: material editor: Mechanical Damage for Traction Separation Laws: Quade Damage, Maxe Damage, Quads Damage, or Maxs Damage: Direction relative to local 1-direction (for XFEM): Normal or Parallel |
The maximum principal stress criterion can be represented as
represents the maximum allowable principal stress. The symbol 
represents the Macaulay bracket with the usual interpretation (i.e., 
if 
and 
if 
). The Macaulay brackets are used to signify that a purely compressive stress state does not initiate damage. Damage is assumed to initiate when the maximum principal stress ratio (as defined in the expression above) reaches a value of one. | Input File Usage: | *DAMAGE INITIATION, CRITERION=MAXPS |
| Abaqus/CAE Usage: | Property module: material editor: Mechanical: Damage for Traction Separation Laws: Maxps Damage |
The maximum principal strain criterion can be represented as
represents the maximum allowable principal strain, and the Macaulay brackets signify that a purely compressive strain does not initiate damage. Damage is assumed to initiate when the maximum principal strain ratio (as defined in the expression above) reaches a value of one.| Input File Usage: | *DAMAGE INITIATION, CRITERION=MAXPE |
| Abaqus/CAE Usage: | Property module: material editor: Mechanical: Damage for Traction Separation Laws: Maxpe Damage |
The maximum nominal stress criterion can be represented as
, consists of three components (two in two-dimensional problems). 
is the component normal to the likely cracked surface, and 
and 
are the two shear components on the likely cracked surface. Depending on what you specify (see “Specifying the crack direction,” above), the likely cracked surface will be orthogonal either to the element local 1-direction or to the element local 2-direction. Here, 
, 
, and 
represent the peak values of the nominal stress. The symbol represents the Macaulay bracket with the usual interpretation. The Macaulay brackets are used to signify that a purely compressive stress state does not initiate damage. Damage is assumed to initiate when the maximum nominal stress ratio (as defined in the expression above) reaches a value of one. | Input File Usage: | *DAMAGE INITIATION, CRITERION=MAXS |
| Abaqus/CAE Usage: | Property module: material editor: Mechanical: Damage for Traction Separation Laws: Maxs Damage |
The maximum nominal strain criterion can be represented as
| Input File Usage: | *DAMAGE INITIATION, CRITERION=MAXE |
| Abaqus/CAE Usage: | Property module: material editor: Mechanical: Damage for Traction Separation Laws: Maxe Damage |
The quadratic nominal stress criterion can be represented as
| Input File Usage: | *DAMAGE INITIATION, CRITERION=QUADS |
| Abaqus/CAE Usage: | Property module: material editor: Mechanical: Damage for Traction Separation Laws: Quads Damage |
The quadratic nominal strain criterion can be represented as
| Input File Usage: | *DAMAGE INITIATION, CRITERION=QUADE |
| Abaqus/CAE Usage: | Property module: material editor: Mechanical: Damage for Traction Separation Laws: Quade Damage |
User subroutine UDMGINI provides a general capability for implementing a user-defined damage initiation criterion.
You can define several damage initiation mechanisms in user subroutine UDMGINI. You represent each damage initiation mechanism by a fracture criterion, 
, and its associated normal direction to the crack plane or the crack line. Although you can define several damage initiation mechanisms, the actual damage initiation for an enriched element is governed by the most severe damage initiation mechanism:
You must specify any material constants that are needed in user subroutine UDMGINI as part of a user-defined damage initiation criterion definition.
| Input File Usage: | Use the following option to define a user-defined damage initiation criterion: |
*DAMAGE INITIATION, CRITERION=USER Use the following option to specify the total number of failure mechanisms in the user-defined damage initiation criterion: *DAMAGE INITIATION, CRITERION=USER, FAILURE MECHANISMS= Use the following option to define properties for a user-defined damage initiation criterion: *DAMAGE INITIATION, CRITERION=USER, PROPERTIES=number_of_constants |
| Abaqus/CAE Usage: | Defining a user-defined damage initiation criterion is not supported in Abaqus/CAE. |
The damage evolution law describes the rate at which the cohesive stiffness is degraded once the corresponding initiation criterion is reached. The general framework for describing the evolution of damage is conceptually similar to that used for damage evolution in surface-based cohesive behavior (“Surface-based cohesive behavior,” Section 35.1.10).
A scalar damage variable, D, represents the averaged overall damage at the intersection between the crack surfaces and the edges of cracked elements. It initially has a value of 0. If damage evolution is modeled, D monotonically evolves from 0 to 1 upon further loading after the initiation of damage. The normal and shear stress components are affected by the damage according to
, 
, and 
are the normal and shear stress components predicted by the elastic traction-separation behavior for the current separations without damage.To describe the evolution of damage under a combination of normal and shear separations across the interface, an effective separation is defined as
| Input File Usage: | Use the following option to specify a damage evolution law: |
*DAMAGE EVOLUTION |
| Abaqus/CAE Usage: | Property module: material editor: MechanicalDamage for Traction Separation Laws: Maxpe Damage or Maxps Damage: SuboptionsDamage Evolution |
A separate damage evolution law should be specified for each damage initiation criterion defined in user subroutine UDMGINI. Each combination of a damage initiation criterion and a corresponding damage evolution law is referred to as a failure mechanism. Damage will accumulate for only one failure mechanism per element, corresponding to the mechanism whose damage initiation criterion was achieved first.
| Input File Usage: | Use the following options to specify damage evolution laws for multiple user-defined damage initiation criteria: |
*DAMAGE INITIATION, CRITERION=USER, FAILURE MECHANISMS= |
| Abaqus/CAE Usage: | Defining a user-defined damage initiation criterion is not supported in Abaqus/CAE. |
Models exhibiting various forms of softening behavior and stiffness degradation often lead to severe convergence difficulties in Abaqus/Standard. Viscous regularization of the constitutive equations defining cohesive behavior in an enriched element can be used to overcome some of these convergence difficulties. Viscous regularization damping causes the tangent stiffness matrix to be positive definite for sufficiently small time increments.
The approximate amount of energy associated with viscous regularization over the whole model is available using output variable ALLVD.
| Input File Usage: | Use the following option to specify viscous regularization: |
*DAMAGE STABILIZATION |
| Abaqus/CAE Usage: | Property module: material editor: MechanicalDamage for Traction Separation Laws: Quade Damage, Maxe Damage, Quads Damage, Maxs Damage, Maxpe Damage, or Maxps Damage: SuboptionsDamage Stabilization Cohesive |
The formulae and laws that govern the behavior of the XFEM-based linear elastic fracture mechanics approach for crack propagation analysis are very similar to those used for modeling delamination along a known and partially bonded surface (see “Crack propagation analysis,” Section 11.4.3), where the strain energy release rate at the crack tip is calculated based on the modified Virtual Crack Closure Technique (VCCT). However, unlike this method, the XFEM-based LEFM approach can be used to simulate crack propagation along an arbitrary, solution-dependent path in the bulk material with or without an initial crack. You complete the definition of the crack propagation capability by defining a fracture-based surface behavior and specifying the fracture criterion in enriched elements.
By definition, the XFEM-based LEFM approach inherently requires the presence of a crack in the model since it is based on the principles of linear elastic fracture mechanics. The crack can be pre-existing, or it can nucleate during the analysis. If there is no pre-existing crack for a given enriched region, the XFEM-based LEFM approach is not activated until a crack nucleates. The crack nucleation is governed by one of the six built-in stress- or strain-based crack initiation criteria or a user-defined crack initiation criterion discussed in “Crack initiation and direction of crack extension,” above. After a crack is nucleated in an enriched region, subsequent propagation of the crack is governed by the XFEM-based LEFM criterion.
| Input File Usage: | Use the following option to specify the crack nucleation criterion as part of the material definition when there is no pre-existing crack in an enriched region: |
*DAMAGE INITIATION, TOLERANCE= |
| Abaqus/CAE Usage: | Property module: material editor: Mechanical: Damage for Traction Separation Laws: Quade Damage, Maxe Damage, Quads Damage, Maxs Damage, Maxpe Damage, or Maxps Damage: |
If there is a pre-existing crack in an enriched region, the crack extends after an equilibrium increment when the fracture criterion, f, reaches the value 1.0 within a given tolerance:
. If , the time increment is cut back such that the crack extension criterion is satisfied. The default value of is 0.2.| Input File Usage: | Use both of the following options: |
*SURFACE BEHAVIOR *FRACTURE CRITERION, TOLERANCE= |
| Abaqus/CAE Usage: | Interaction module: InteractionPropertyCreate, Contact, MechanicalFracture Criterion, Tolerance: |
You must specify the crack propagation direction when the fracture criterion is satisfied. The crack can extend at a direction normal to the direction of the maximum tangential stress, orthogonal to the element local 1-direction (see “Conventions,” Section 1.2.2), or orthogonal to the element local 2-direction. By default, the crack propagates normal to the direction of the maximum tangential stress.
| Input File Usage: | Use one of the following options to specify the crack direction when the fracture criterion is satisfied: |
*FRACTURE CRITERION, NORMAL DIRECTION=MTS (default) *FRACTURE CRITERION, NORMAL DIRECTION=1 *FRACTURE CRITERION, NORMAL DIRECTION=2 |
| Abaqus/CAE Usage: | Interaction module: contact property editor: MechanicalFracture Criterion: Direction of crack growth relative to local 1-direction: Maximum tangential stress, Normal, or Parallel |
Abaqus provides three common mode-mix formulae for computing the equivalent fracture energy release rate 
: the BK law, the power law, and the Reeder law models. The choice of model is not always clear in any given analysis; an appropriate model is best selected empirically.
The BK law model is described in Benzeggagh and Kenane (1996) by the following formula:
To define this model, you must provide 
and 
. This model provides a power law relationship combining energy release rates in Mode I, Mode II, and Mode III into a single scalar fracture criterion.
| Input File Usage: | *FRACTURE CRITERION, TYPE=VCCT, MIXED MODE BEHAVIOR=BK |
| Abaqus/CAE Usage: | Interaction module: contact property editor: MechanicalFracture Criterion: Mixed mode behavior: BK, and enter the critical energy release rates in the data table |
The power law model is described in Wu and Reuter (1965) by the following formula:
To define this model, you must provide 
and 
.
| Input File Usage: | *FRACTURE CRITERION, TYPE=VCCT, MIXED MODE BEHAVIOR=POWER |
| Abaqus/CAE Usage: | Interaction module: contact property editor: MechanicalFracture Criterion: Mixed mode behavior: Power, and enter the critical energy release rates in the data table |
The Reeder law model is described in Reeder et al. (2002) by the following formula:
To define this model, you must provide 
and . The Reeder law is best applied when 
; when 
, the Reeder law reduces to the BK law. The Reeder law applies only to three-dimensional problems.
| Input File Usage: | *FRACTURE CRITERION, TYPE=VCCT, MIXED MODE BEHAVIOR=REEDER |
| Abaqus/CAE Usage: | Interaction module: contact property editor: MechanicalFracture Criterion: Mixed mode behavior: Reeder, and enter the critical energy release rates in the data table |
You can define a VCCT criterion with varying energy release rates by specifying the critical energy release rates at the nodes.
If you indicate that the nodal critical energy rates will be specified, any constant critical energy release rates you specify are ignored and the critical energy release rates are interpolated from the nodes. The critical energy release rates must be defined at all nodes in the enriched region.
| Input File Usage: | Use both of the following options: |
*FRACTURE CRITERION, TYPE=VCCT, NODAL ENERGY RATE *NODAL ENERGY RATE |
| Abaqus/CAE Usage: | Defining a VCCT criterion with varying energy release rates is not supported in Abaqus/CAE. |
If you specify the low-cycle fatigue criterion, progressive crack growth at the enriched elements subjected to sub-critical cyclic loading can be simulated. This criterion can be used only in a low-cycle fatigue analysis using the direct cyclic approach (“Low-cycle fatigue analysis using the direct cyclic approach,” Section 6.2.7). A low-cycle fatigue step can be the only step, can follow a general static step, or can be followed by a general static step. You can include multiple low-cycle fatigue analysis steps in a single analysis. If you perform a fatigue analysis in a model without a pre-existing crack, you must precede the fatigue step with a static step that nucleates a crack, as discussed in “Crack nucleation and direction of crack extension.”
The onset and fatigue crack growth are characterized by using the Paris law, which relates the relative fracture energy release rate to crack growth rates as illustrated in Figure 10.7.1–3. The fracture energy release rates at the crack tips in the enriched elements are calculated based on the above mentioned VCCT technique.
The Paris regime is bounded by the energy release rate threshold, 
, below which there is no consideration of fatigue crack initiation or growth, and the energy release rate upper limit, 
, above which the fatigue crack will grow at an accelerated rate. 
is the critical equivalent strain energy release rate calculated based on the user-specified mode-mix criterion and the fracture strength of the bulk material. The formulae for calculating have been provided above for different mixed mode fracture criteria. You can specify the ratio of over and the ratio of over . The default values are 
and 
.
| Input File Usage: | Use both of the following options: |
*SURFACE BEHAVIOR *FRACTURE CRITERION, TYPE=FATIGUE |
| Abaqus/CAE Usage: | Specifying a low-cycle fatigue criterion is not supported in Abaqus/CAE. |
The onset of fatigue crack growth refers to the beginning of fatigue crack growth at the crack tip in the enriched elements. In a low-cycle fatigue analysis the onset of the fatigue crack growth criterion is characterized by 
, which is the relative fracture energy release rate when the structure is loaded between its maximum and minimum values. The fatigue crack growth initiation criterion is defined as
and 
are material constants and 
is the cycle number. The enriched elements ahead of the crack tips will not be fractured unless the above equation is satisfied and the maximum fracture energy release rate, 
, which corresponds to the cyclic energy release rate when the structure is loaded up to its maximum value, is greater than .Once the onset of the fatigue crack growth criterion is satisfied at the enriched element, the crack growth rate, 
, can be calculated based on the relative fracture energy release rate, . The rate of the crack growth per cycle is given by the Paris law if 
and 
are material constants.At the end of cycle , Abaqus/Standard extends the crack length, 
, from the current cycle forward over an incremental number of cycles, 
to 
by fracturing at least one enriched element ahead of the crack tips. Given the material constants and , combined with the known element length and the likely crack propagation direction 
at the enriched elements ahead of the crack tips, the number of cycles necessary to fail each enriched element ahead of the crack tip can be calculated as 
, where j represents the enriched element ahead of the 
th crack tip. The analysis is set up to advance the crack by at least one enriched element after the loading cycle is stabilized. The element with the fewest cycles is identified to be fractured, and its 
is represented as the number of cycles to grow the crack equal to its element length, 
. The most critical element is completely fractured with a zero constraint and a zero stiffness at the end of the stabilized cycle. As the enriched element is fractured, the load is redistributed and a new relative fracture energy release rate must be calculated for the enriched elements ahead of the crack tips for the next cycle. This capability allows at least one enriched element ahead of the crack tips to be fractured completely after each stabilized cycle and precisely accounts for the number of cycles needed to cause fatigue crack growth over that length.
If 
, the enriched elements ahead of the crack tips will be fractured by increasing the cycle number count, 
, by one only.
The simulation of structures with unstable propagating cracks is challenging and difficult. Nonconvergent behavior may occur from time to time. Localized damping is included for the XFEM-based LEFM approach by using the viscous regularization technique. Viscous regularization damping causes the tangent stiffness matrix of the softening material to be positive for sufficiently small time increments.
| Input File Usage: | *FRACTURE CRITERION, TYPE=VCCT, VISCOSITY= |
| Abaqus/CAE Usage: | Interaction module: contact property editor: MechanicalFracture Criterion: Viscosity:  |
Because the mesh is not required to conform to the geometric discontinuities, the initial location of a pre-existing crack must be specified in the model. The level set method is provided for this purpose. Two signed distance functions per node are generally required to describe a crack geometry. The first describes the crack surface, while the second is used to construct an orthogonal surface so that the intersection of the two surfaces gives the crack front (see “Initial conditions in Abaqus/Standard and Abaqus/Explicit,” Section 32.2.1).
The first signed distance function must be either greater or less than zero and cannot be equal to zero. If an initial crack has to be defined at the boundaries of an element, a very small positive or negative value for the first signed distance function must be specified.
| Input File Usage: | Use the following option to specify the initial location of an enriched feature: |
*INITIAL CONDITIONS, TYPE=ENRICHMENT |
| Abaqus/CAE Usage: | Interaction module: crack editor: Crack location: Select: select region |
The crack propagation capability can be activated or deactivated within the step definition.
| Input File Usage: | Use the following option to activate the crack propagation capability within the step definition: |
*ENRICHMENT ACTIVATION, NAME=name, ACTIVATE=ON (default) Use the following option to deactivate the crack propagation capability within the step definition: *ENRICHMENT ACTIVATION, NAME=name, ACTIVATE=OFF |
| Abaqus/CAE Usage: | To modify the status of the crack propagation capability in a step, you must first create an XFEM crack growth interaction: |
Interaction module: Create Interaction: select initial step: XFEM Crack Growth: select crack: Interaction manager: select interaction in step: Edit: toggle on/off Allow crack growth in this step |
When you evaluate the contour integrals using the conventional finite element method (“Contour integral evaluation,” Section 11.4.2), you must define the crack front explicitly and specify the virtual crack extension direction in addition to matching the mesh to the cracked geometry. Detailed focused meshes are generally required and obtaining accurate contour integral results for a crack in a three-dimensional curved surface can be cumbersome. The extended finite element in conjunction with the level set method alleviates these shortcomings. The adequate singular asymptotic fields and the discontinuity are ensured by the special enrichment functions in conjunction with additional degrees of freedom. In addition, the crack front and the virtual crack extension direction are determined automatically by the level set signed distance functions.
| Input File Usage: | Use the following option to obtain contour integral for a named enriched feature with the extended finite element method: |
*CONTOUR INTEGRAL, XFEM, CRACK NAME=name |
| Abaqus/CAE Usage: | Step module: history output request editor: Domain: Crack: crack name |
Although XFEM has alleviated the shortcomings associated with refining the mesh in the neighborhood of the crack front due to the added asymptotic fields, you must generate a sufficient number of elements around the crack front to obtain path-independent contours. The group of elements within a small radius from the crack front are enriched and become involved in the contour integral calculations. The default enrichment radius is three times the typical element characteristic length in the enriched area. You must include the elements inside the enrichment radius in the element set used to define the enriched region.
| Input File Usage: | Use the following option to specify an enrichment radius: |
*ENRICHMENT, ENRICHMENT RADIUS |
| Abaqus/CAE Usage: | Interaction module: crack editor: Enrichment radius: Analysis default or Specify |
Modeling discontinuities as an enriched feature can be performed using the static procedure (see “Static stress analysis,” Section 6.2.2), the implicit dynamic procedure (see “Implicit dynamic analysis using direct integration,” Section 6.3.2), or the low-cycle fatigue analysis using the direct cyclic approach (“Low-cycle fatigue analysis using the direct cyclic approach,” Section 6.2.7).
Initial conditions to identify initial boundaries or interfaces of an enriched feature can be specified (see “Initial conditions in Abaqus/Standard and Abaqus/Explicit,” Section 32.2.1).
Boundary conditions can be applied to any of the displacement degrees of freedom (see “Boundary conditions in Abaqus/Standard and Abaqus/Explicit,” Section 32.3.1).
The following types of loading can be prescribed in a model with an enriched feature:
Concentrated nodal forces can be applied to the displacement degrees of freedom (1–3); see “Concentrated loads,” Section 32.4.2.
Distributed pressure forces or body forces can be applied; see “Distributed loads,” Section 32.4.3. The distributed load types available with particular elements are described in Part VI, “Elements.”
The following predefined fields can be specified in a model with an enriched feature, as described in “Predefined fields,” Section 32.6.1:
Nodal temperatures (although temperature is not a degree of freedom in stress/displacement elements). The specified temperature affects temperature-dependent critical stress and strain failure criteria.
The values of user-defined field variables. The specified value affects field-variable-dependent material properties.
Any of the mechanical constitutive models in Abaqus/Standard, including user-defined materials (defined using user subroutine “UMAT,” Section 1.1.40 of the Abaqus User Subroutines Reference Manual) can be used to model the mechanical behavior of the enriched element in a crack propagation analysis. See Part V, “Materials.” The inelastic definition at a material point must be used in conjunction with the linear elastic material model (“Linear elastic behavior,” Section 21.2.1), the porous elastic material model (“Elastic behavior of porous materials,” Section 21.3.1), or the hypoelastic material model (“Hypoelastic behavior,” Section 21.4.1). Only isotropic elastic materials are supported when evaluating the contour integral for a stationary crack.
Only first-order solid continuum stress/displacement elements and second-order stress/displacement tetrahedron elements can be associated with an enriched feature. For propagating cracks these include bilinear plane strain and plane stress elements, linear brick elements, linear tetrahedron elements, and second-order tetrahedron elements. For stationary cracks, these include linear brick elements, linear tetrahedron elements, and second-order tetrahedron elements.
For an incompatible mode element, Abaqus/Standard discards the contribution due to the incompatible deformation mode immediately after the element is fractured under a tensile loading. Therefore, the stress level at the cracked element may not return completely to its originally unloaded state even when this cracked element is unloaded completely and the contact of the cracked surfaces is reestablished.
In addition to the standard output identifiers available in Abaqus (“Abaqus/Standard output variable identifiers,” Section 4.2.1), the following variables have special meaning for a model with an enriched feature:
PHILSM | Signed distance function to describe the crack surface. |
PSILSM | Signed distance function to describe the initial crack front. |
STATUSXFEM | Status of the enriched element. (The status of an enriched element is 1.0 if the element is completely cracked and 0.0 if the element contains no crack. If the element is partially cracked, the value of STATUSXFEM lies between 1.0 and 0.0.) |
ENRRTXFEM | All components of strain energy release rate when linear elastic fracture mechanics with the extended finite element method is used. |
A crack can be visualized through the iso-surface for the signed distance function PHILSM.
If a crack cuts through a very tiny corner of an enriched element, the displacements along the crack front in the enriched element may be distorted in rare cases in the Visualization module of Abaqus/CAE (Abaqus/Viewer) when displaying the contours. The distortion, however, is not present when viewing only the deformed shape.
The following limitations exist with an enriched feature:
An enriched element cannot be intersected by more than one crack.
A crack is not allowed to turn more than 90° in one increment during an analysis.
Only asymptotic crack-tip fields in an isotropic elastic material are considered for a stationary crack.
Adaptive remeshing is not supported.
The following is an example of modeling crack propagation with the XFEM-based cohesive segments method:
*HEADING ... *NODE, NSET=ALL ... *ELEMENT, TYPE=C3D8, ELSET=REGULAR *ELEMENT, TYPE=C3D8, ELSET=ENRICHED ... *SOLID SECTION, MATERIAL=STEEL1, ELSET=REGULAR *SOLID SECTION, MATERIAL=STEEL12, ELSET=ENRICHED *ENRICHMENT, TYPE=PROPAGATION CRACK, ELSET=ENRICHED, NAME=ENRICHMENT, INTERACTION=INTERACTION *MATERIAL, NAME=STEEL1 ... *MATERIAL, NAME=STEEL2 *DAMAGE INITIATION, CRITERION=MAXPS, TOLERANCE=0.05 *DAMAGE EVOLUTION, TYPE=ENERGY Data lines to specify the failure mechanism ... *SURFACE INTERACTION, NAME=INTERACTION *SURFACE BEHAVIOR Data lines to specify the contact of cracked element surfaces ... *STEP *STATIC ... *END STEP *STEP *STATIC ... *ENRICHMENT ACTIVATION, TYPE=PROPAGATION CRACK, NAME=ENRICHMENT, ACTIVATE=OFF ... *END STEP
The following is an example of modeling crack propagation with the XFEM-based LEFM approach:
*HEADING ... *NODE, NSET=ALL ... *ELEMENT, TYPE=C3D8, ELSET=REGULAR *ELEMENT, TYPE=C3D8, ELSET=ENRICHED ... *SOLID SECTION, MATERIAL=STEEL1, ELSET=REGULAR *SOLID SECTION, MATERIAL=STEEL12, ELSET=ENRICHED *ENRICHMENT, TYPE=PROPAGATION CRACK, ELSET=ENRICHED, NAME=ENRICHMENT, INTERACTION=INTERACTION *MATERIAL, NAME=STEEL1 ... *MATERIAL, NAME=STEEL2 *DAMAGE INITIATION, CRITERION=MAXPS, TOLERANCE=0.05 Data lines to specify the crack nucleation mechanism ... *SURFACE INTERACTION, NAME=INTERACTION *SURFACE BEHAVIOR *FRACTURE CRITERION, TYPE=VCCT, TOLERANCE=0.05,VISCOSITY=0.00001 Data lines to specify the crack propagation criterion ... *END STEP
The following is an example of calculating contour integrals in stationary cracks with the extended finite element method:
*HEADING ... *NODE, NSET=ALL ... *ELEMENT, TYPE=C3D8, ELSET=REGULAR *ELEMENT, TYPE=C3D8, ELSET=ENRICHED ... *SOLID SECTION, MATERIAL=STEEL1, ELSET=REGULAR *SOLID SECTION, MATERIAL=STEEL12, ELSET=ENRICHED *ENRICHMENT, TYPE=STATIONARY CRACK, ELSET=ENRICHED, NAME=ENRICHMENT, ENRICHMENT RADIUS *MATERIAL, NAME=STEEL1 ... *MATERIAL, NAME=STEEL2 ... *STEP *STATIC ... *CONTOUR INTEGRAL, CRACK NAME=ENRICHMENT, XFEM *END STEP
Belytschko, T., and T. Black, “Elastic Crack Growth in Finite Elements with Minimal Remeshing,” International Journal for Numerical Methods in Engineering, vol. 45, pp. 601–620, 1999.
Benzeggagh, M., and M. Kenane, “Measurement of Mixed-Mode Delamination Fracture Toughness of Unidirectional Glass/Epoxy Composites with Mixed-Mode Bending Apparatus,” Composite Science and Technology, vol. 56 439, 1996.
Elguedj, T., A. Gravouil, and A. Combescure, “Appropriate Extended Functions for X-FEM Simulation of Plastic Fracture Mechanics,” Computer Methods in Applied Mechanics and Engineering, vol. 195, pp. 501–515, 2006.
Melenk, J., and I. Babuska, “The Partition of Unity Finite Element Method: Basic Theory and Applications,” Computer Methods in Applied Mechanics and Engineering, vol. 39, pp. 289–314, 1996.
Reeder, J., S. Kyongchan, P. B. Chunchu, and D. R.. Ambur, “Postbuckling and Growth of Delaminations in Composite Plates Subjected to Axial Compression”43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Denver, Colorado, vol. 1746, p. 10, 2002.
Remmers, J. J. C., R. de Borst, and A. Needleman, “The Simulation of Dynamic Crack Propagation using the Cohesive Segments Method,” Journal of the Mechanics and Physics of Solids, vol. 56, pp. 70–92, 2008.
Song, J. H., P. M. A. Areias, and T. Belytschko, “A Method for Dynamic Crack and Shear Band Propagation with Phantom Nodes,” International Journal for Numerical Methods in Engineering, vol. 67, pp. 868–893, 2006.
Sukumar, N., Z. Y. Huang, J.-H. Prevost, and Z. Suo, “Partition of Unity Enrichment for Bimaterial Interface Cracks,” International Journal for Numerical Methods in Engineering, vol. 59, pp. 1075–1102, 2004.
Sukumar, N., and J.-H. Prevost, “Modeling Quasi-Static Crack Growth with the Extended Finite Element Method Part I: Computer Implementation,” International Journal for Solids and Structures, vol. 40, pp. 7513–7537, 2003.
Wu, E. M., and R. C. Reuter Jr., “Crack Extension in Fiberglass Reinforced Plastics,” T and M Report, University of Illinois, vol. 275, 1965.
